Компьютер − вот наш «современный чародей», наш Бог и высшее проявление человеческого гения. Но именно компьютер несет угрозу существованию самого человечества. Чем мощнее и производительней становятся компьютеры, чем сложнее задачи, которые они решают, тем эта угроза становится сильнее и реальнее.
    
     Типы информации
    
     Существует два типа информации − образная и числовая. Обработка информации есть мышление. Биологические объекты, в том числе и человек, воспринимают образную информацию. Компьютеры работают с числовой информацией. Таким образом, существует два типа мышлений.
     Слово есть имя образа. Оно возникло из дочеловеческих образных представлений − криков, жестов, иных действий животных как реакции на некоторые образы. «Вначале было слово, и слово было от Бога». А числа нет в исходном человеческом мышлении.
     Компьютер трудно научить воспринимать и обрабатывать образную информацию, а человек долго шел к разработке и освоению числовой. Это был длительный процесс и он, по нашему мнению, не закончился.
    
     Числовые эпохи
    
     В процессе своего цивилизационного развития человечество прошло целый ряд числовых эпох. Каждая числовая эпоха характеризуется новым понятием числа и своими приемами работы с ними − вычислительной технологией.
     Предшествующие понятия числа при смене эпох могут использоваться, а могут и отбрасываться.
    
     Первая числовая эпоха − эпоха натурального числа
    
     В эту эпоху числа представлялись набором предметов − пальцами, камушками, бусинками и т.д. Действия над числами осуществлялись посредством действий над предметами. В конце этого периода возникли изображения чисел и простейшие действия над ними в письменной форме. Четки, русские счеты, сгибание и разгибание пальцев при перечислениях − все это атавизмы той, древнейшей числовой эпохи.
    
     Вторая числовая эпоха − эпоха дробных чисел
    
     Но постепенно человечество вошло в новую числовую эпоху. Целых чисел уже не хватало для потребностей человека. Прежде всего, для исчисления времени. Во вторую числовую эпоху было создано понятие нецелого числа. Этому этапу соответствует римская (аддитивная) система счисления (представления) чисел. Действия над ними стали предметом особой науки − арифметики, которая до сих пор изучается в школе. В эту эпоху получило большое развитие астрономия и счисление времени, рассчитывались уже достаточно сложные машины − катапульты, например и т.д.
    
     Третья числовая эпоха − эпоха действительных и приближенных чисел
    
     Однако дробные числа не могли удовлетворить все возрастающие потребности человечества в обработке числовой информации. Ведь в те времена человек, знающий четыре действия над дробными числами смело мог претендовать на научное звание, соответствующее нынешнему доктору наук. И возникла новая числовая эпоха, инициированная позиционной (арабской) системой представления чисел. Третья числовая эпоха − это пир, праздник математики. Практически вся теоретическая математика, изучаемая в институтах и используемая на практике, возникла именно в эту эпоху. В теоретической математике центральное место приобрело понятие действительного или вещественного числа, образно представляемого точкой, не имеющей своих размеров на линии, числовой оси. Для практических вычислительных целей было создано понятие приближенного числа и разработаны правила действий с ними − «Правила приближенных вычислений». Это очень простые, не удивительно эффективные правила, которые позволили с весьма скромными вычислительными средствами ручного счета решать чрезвычайно сложные задачи. Достаточно только упомянуть о разработке разнообразных машин, сложнейших сооружения, даже атомная бомба и космические полеты на первых шагах создавались в рамках именно этой числовой эпохи.
     Люди старшего поколения хорошо помнят те правила приближенных вычислений, что размещались на одной страничке школьных таблиц Брадиса. И наверное еще помнят, как они вручную с помощью этих правил решали треугольники по тригонометрии. Увы, современные инженеры, математики и даже программисты не знают, что такое приближенное число.
     И именно третья числовая эпоха, новая система числовой обработки явилась основой промышленной революции семнадцатого века. В рамках дробных чисел она вряд смогла бы состояться. Вот что такое адекватное потребностям человеческой практики понятие числа.
    
     Четвертая числовая эпоха − компьютерная эпоха
     Это уже современная эпоха. Она характеризуется использованием компьютеров − небиологических средств мышления (обработки информации) на основе кристаллов. Компьютер потребовал использования двоичного (вместо антропного десятичного) представления чисел. В эту эпоху вычислительные возможности человечества возросли на много порядков. Это период расцвета вычислительной математики. Хотя в сфере теоретической математики она мало что внесла нового.
    
     Числовые особенности четвертой числовой эпохи
    
     Основные вычислительные понятия предшествующей числовой эпохи − понятие приближенного числа и действия с ними − были отброшено. В качестве главного понятия стало использоваться понятие рационального числа (числа с плавающей точкой в компьютерной терминологии).
    
     Компьютерные числа
    
     В компьютерах используются следующие типы чисел:
     1. Натуральные и целые числа. К работе с ними нет претензий.
     2. Нецелые числа используются в формате чисел с плавающей точкой (стандарт IEEE 754). С математической точки зрения действительные, вещественные числа, которые использовались в теоретической математики предшествующей числовой эпохи, которые можно представить конечным числом разрядов. Такие числа называют еще рациональными. В зависимости от условий «представимости» существует множество рациональных чисел. Стандарт IEEE 754 фиксирует три таких множества чисел − обычной, двойной и расширенной точности. (Правда, непонятно, причем тут точность, ведь точность есть характеристика не числа, а взаимоотношений. Еще более странно название «вещественные» для невещественной (информационной) институции).
    
     Сопоставление действий над приближенными и рациональными числами
    
     А теперь сопоставим результаты вычислений одних и тех же, по крайней мере, в записи, чисел по «Правилам приближенных чисел» и с помощью компьютера. Мы будем использовать калькулятор MS WINDOWS в формате чисел повышенной точности. В таблице приведены результаты вычислений.
    

    
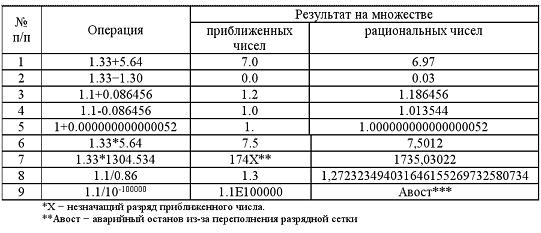
     Вывод: числа и вычислительная математика в этих эпохах различны.
     И возникает вопрос: какое понятие числа и какая система обработки чисел являются более корректными и практически ценными?
     Ответ однозначен. Хотя понятие числа третьей числовой эпохи не вполне совершенно, но нынешнее понятие есть концептуальный шаг назад.
    
     Главная аксиома современной числовой эпохи
    
     Большинство теоретических моделей формулируются на множестве действительных чисел. Но вычислительная их реализация осуществляется на множествах рациональных чисел. При этом неявно предполагается, что возникающие при этом ошибки малы и не существенны для практики. Это есть главная аксиома четвертой числовой эпохи, принимаемая молчаливо и без доказательств. Эта аксиома НЕВЕРНА.
    
     Примеры неверности главной аксиомы четвертой числовой эпохи
    

    
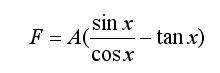
     Любой пятиклассник скажет, что это выражение есть чистый нуль, потому как тангенс и есть отношение синуса и косинуса. Но это на множестве действительных чисел. Но если мы будем вычислять это выражение на компьютере, то получим некоторый ненулевой результат. А выбрав некоторую константу А, можем получить любое желаемое нами число. Например, прнняв аргумент функций равным 30 градусов, а коэффициент A равным сто триллионов, получаем результат вычислений на компьютере F=23.98002. Итак, результаты вычислений на множестве действительных чисел (в теории) и на множестве компьютерных чисел могут быть абсолютно различны.
     Мы могли бы привести еще очень много примеров, когда теоретические значения абсолютно (в тысячи, миллионы, триллионы раз) не совпадают с теми значениями, которые дает компьютер.
     Ограничимся только пример из монографии Клатте Р.,Кулиш У.,Неага М.,Рац Д.,Улльрих Х. PASCAL-XSC. Язык численного программирования. пер. с англ. РХД, 2006.
     Пусть x и у векторы.
    

    
     В точной арифметике:
    

    
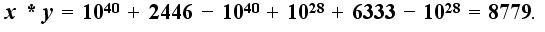
     Однако арифметика чисел с плавающей точкой на любом современном компьютере для такого скалярного произведения дает нулевое значение 0.
     Примерам больших относительных и абсолютных ошибок и полной несопоставимости результатов вычислений на множествах действительных и рациональных чисел несть числа. А это означает, что нет и не может быть полного доверия компьютерным вычислениям даже при исправной технике и проверенных программах. Эти вычислительные ошибки почти не прогнозируемы и не идентифицируемы. Вот почему ответственность за множество технических и промышленных аварий и катастроф некоторые ученые возлагают на компьютерные вычислительные ошибки, в основе которых современное компьютерное представление чисел. Директор Американского института математики на своем сайте www.ima.umn.edu/~arnold/disasters/disasters.html приводит целый ряд аварий и катастроф с миллиардными убытками и человеческими жертвами, которые всецело связаны с существующим понятием компьютерного числа.
     В последнее время мы были свидетелями крупнейших техногенных катастроф − аварии мостов, аквапарков, столкновение самолетов, крушение поездов. Почти всегда причину возлагали на так называемый «человеческий фактор». Но ведь везде использовались в той или иной мере компьютеры. И можем ли мы полностью исключить вероятность вычислительных ошибок (при полностью исправном компьютере и программного обеспечения). Увы, нет, не можем. Причем вероятность таких ошибок растет в прогрессивной степени по мере роста вычислительной мощи компьютеров и усложнения решаемых задач.
    
     Несуществующие числа
    
     Согласно стандарту представления компьютерных рациональных чисел IEEE 754 существует несколько типов представлений с 7, 17 и 21 (десятичными) разрядами.
     Например, калькулятор MS WINDOWS дает
     Log 2=0,30102999566398119521373889472449.
     Существуют ли в человеческой практике или вообще в природе подобные числа? Не существуют. Cовременная числовая эпоха использует попросту несуществующие числа.
     Для сравнения: предшествующая числовая эпоха использовала четырех−пятизначные математические таблицы и лишь в самых высокоточных расчетах − семизначные. Стоит раскрыть любой справочник, чтобы убедиться, что подавляющая часть практических данных имеет 3−5 разрядов. И с этим числовым аппаратом в третью числовую эпоху создавались машины, мосты, небоскребы, атомная бомба, запускались баллистические ракеты и первые спутники.
    
     Ненужные числа
    
     Все нецелые (за исключением денежных) числа имеют прямо или косвенно своим источником измерение. Выходные числа с компьютера пользователю нужны также для использования в измерительной системе. Но измерительные (метрологические) числа не есть рациональные (действительные, абсолютно точные) числа. Для практической числовой деятельности нужны числа метрологические, т.е. числа, обладающие определенной метрологической характеристикой, например, некоторым разбросом значений, ошибкой. А рациональные абсолютно точные просто не нужны. Современная числовая эпоха использует ненужные для практики числа. Превращение ненужных компьютерных (например, 20-разрядных) чисел в практически нужные и полезные осуществляется на базе человеческой интуиции, каковая может отсутствовать или быть ошибочной.
    
     Компьютер − обработчик шумов
    
     На практике обычно используются числа с тремя-пятью десятичными разрядами. Компьютер обрабатывает 7-20 разрядные. Излишние разряды есть шумовые, они могут составлять до 80 процентов всего информационного массива. Современный компьютер есть обработчик шумов, на их обработку тратится большая часть компьютерных ресурсов. А вред, причиняемый шумами, в информатике хорошо известен.
    
     Теоретико-математическая порочность рациональных чисел
    
     Предшествующие числовые множества с точки зрения теоретической математики составляли алгебру (поле), означающее, что результат алгебраических действий с числами из этих множеств принадлежит этим же множествам. Алгеброй являются множества дробных, действительных и приближенных чисел. Но никакое множество рациональных чисел не образует алгебру и даже хотя бы группу. Это показатель теоретико-математической порочности нынешней числовой эпохи. Даже тривиальное уравнение 3x=1 не имеет решения на множестве компьютерных чисел. Суперформаты есть попытка компенсировать этот органический порок рациональных чисел.
    
     Вывод 1
    
     Современные числа и система их компьютерной обработки являются источником большого числа аварий, катастроф, ошибок, нерациональных трат. Тотальный переход к компьютерному управлению, рост вычислительных мощностей и сложности задач ведет к прогрессивному нарастанию неблагоприятных факторов современного числового представления, может стать угрозой самому существованию человеческой цивилизации.
    
     Вывод 2 − кораблестроителя академика Крылова
    
     Выдающийся советский кораблестроитель ак. А.Н.Крылов утверждал: «Лишний вычисленный разряд есть ошибка». С этой точки зрения вся четвертая числовая эпоха есть одна сплошная ошибка, а компьютер − просто недоразумение.
    
     Достоверные вычисления
    
     Некоторые специалисты уже осознали порочность нынешней числовой эпохи. Результатом стало создание концепции достоверных вычислений. (Отметим, что само по себе термин «достоверные вычисления» несет приговор современному компьютерингу, так как отсюда вытекает недостоверность ВСЕХ обычных вычислений.
     В основе концепции достоверных вычислений лежит использование не самих чисел, числовых интервалов.
     Однако в фундаменте этой технологии по-прежнему лежит рациональное число на стандарте IEEE 754. Это не дает кардинального решения, а лишь ведет к резкому, порой экспоненциальному, росту затрат компьютерных ресурсов и еще большему отрыву числовых институций от требований практики. Кому и где, к примеру, нужен математический интервал (0.001 ÷ 1000.000001)?
    
     Финальный вывод
    
     Цивилизационное развитие уже упирается в барьер нынешнего понятия числа (рационального числа). Задачей номер 1 является создание новой концепции числа и методов его обработки. Это будет величайший историко-цивилизационный поворот, переход в новую числовую эпоху.
     Такой переход будет не менее значим, чем переход от римской системы счисления к арабской, создавшей базу промышленной революции, чем переход от ручного счета к компьютерному, создавшему информационную цивилизацию.
    
     ВЕЛИКИЙ НАЦИОНАЛЬНЫЙ ПРОЕКТ
    
     Россия, российская наука, российская промышленность должна возглавить переход в новую числовую эпоху. На этом пути страну ожидает мировое первенство в компьютерной и иных областях науки, техники и бизнеса.
    
     3.05.08
     Москва